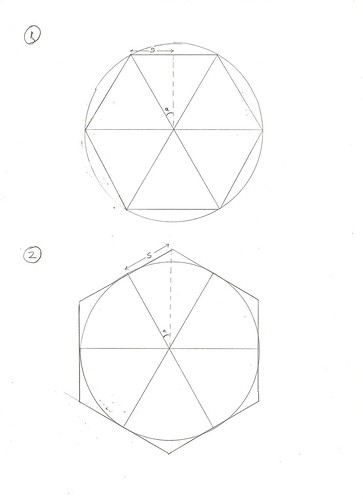
In each of the two diagrams there is a circle of diameter 1. Also in each diagram six equally spaced lines have been drawn from the centre to the edge of the circle (let's call them "spokes")
In diagram 1, the ends of the spokes have been joined up to form a regular hexagon inside the circle. In diagram 2, lines have been drawn perpendicular to the ends of the spokes, forming a hexagon which is outside the circle.
Pi is defined as being the ratio between the circumference and the diameter of a circle. So, in our circles, as the diameter is 1, the circumference equals Pi.
Let's imagine that we don't know what the value of Pi is, but we would like to try to work it out. What we can see from the diagrams is that the perimeter of the hexagon in diagram 1 is less than Pi, and the perimeter of the hexagon in diagram 2 is more than Pi. So, if we can calculate the perimeters of the two hexagons, we will know that the value of Pi lies in between the two numbers.
In diagram 1, the dotted line forms a right angled triangle along with one of the spokes and the length marked s. Given than sin = opposite / hypotenuse, we can see that:
sin a = s / 0.5 (given that each spoke is half of the diameter of the circle).
Also, the angle a is 30 degrees as it is half of the gap between two spokes, and there are six equally spaced spokes (i.e. 360 / 6 / 2 =30).
So, s = 0.5 x sin 30, i.e. s = 0.25.
There are twelve of the lengths s around the hexagon (as s represents half of one side) so that the total perimeter of the hexagon is 0.25 x 12 = 3.
Now, lots of the same logic applies to working out the perimeter of the hexagon in diagram 2, except that this time we need to use tan, as tan = opposite / adjacent.
This time, tan a = s / 0.5
i.e s = 0.5 x tan 30
i.e. s = 0.5 x 0.577 = 0.289
And so, the hexagon in diagram 2 has a perimeter of 3.464.
So, we have been able to show that Pi must be somewhere in between 3 and 3.464.
Now, we didn't have to use hexagons to form our estimates for Pi. We can start the process by drawing any number of equally spaced spokes around our circle.
In fact, let's say that we draw n spokes. Then the first diagram will have an n-agon drawn just inside the circle and the second diagram would have an n-agon drawn just outside the circle.
And, we can calculate the perimeter of each n-agon in exactly the same way as for the hexagon, by constructing a right angled triangle.
For the inside n-agon, the right angled triangle will have half of the gap between two spokes as its angle a in the centre. If there are n spokes, then each spoke is 360/n degrees away from its neighbour, and as angle a is half of that, then angle a will be 180/n. The length s within the n-agon will again be half of a side, and the same formula will be true, that
sin a = s / 0.5, and so s = 0.5 x sin a.
As s is half of one side of the n-agon, then it will be necessary to multiply s by 2n to get the perimeter of the n-agon, so the perimeter will be:
(0.5 x sin a) X 2n = n x sin a, but remembering that a = 180/n, then the perimeter of the n-agon is given by the formula
Perimeter of inside n-agon = n x sin(180/n).
The exact same logic applies to working out the perimeter of the n-agon which sits just outside the circle, so that
Perimeter of outside n-agon = n x tan(180/n).
As n gets bigger, so the spokes get closer and closer together and so each of the n-agons inside and outside the circle get closer to it, meaning that their perimeters get closer and closer to equalling Pi.
Or to put it another way,
If a = n x sin(180/n), and b = n x tan(180/n), then as n gets bigger and bigger, so a increases towards Pi and b decreases towards Pi.
For n=2000, a=3.1415913617 and b=3.1415952374.